The solution to the problem described below was provided by Jay Petrulis in a posting at http://www.mrexcel.com/board2/viewtopic.php?p=355022#355022. In this write up, the procedural programming solution is redone from an object oriented perspective. The reader should not interpret this to mean that OOP solutions are written in the conventional manner and subsequently translated into OOP. Quite the contrary. The OOP paradigm is so different from that of procedural programming that translation from one to the other is definitely not recommended! The solution below was designed from scratch while, of course, sharing the underlying mathematics and trigonometry analysis with Jay’s solution.
The problem at hand is to find the coordinates of the center of the circle given two points on the circumference and the radius. Basically, in Figure 1, given the location of points P0 and P1 and the radius R, what is the location of point C? Of course, this chapter is not about geometry and trigonometry. The focus is on developing an object oriented solution; the underlying mathematics will be taken as given.
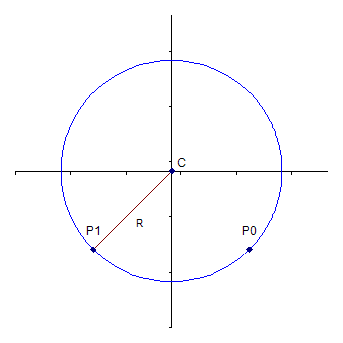
Figure 1
A point is a type of object, and hence should be a class of its own. However, Excel already has an object named point – it is part of a series in a chart. Rather than use a name that will conflict with Excel’s Point, we will call this object a GeoPoint (for Geometric Point).
What are the key properties of a point? Absolutely critical would be the coordinates – given by a point’s x and its y values. In addition, other properties that will be of use are distance of another point from this point, the coordinate of the midpoint between this point and another point, and the slope of the line connecting this point with another point.
Create a class module, name it GeoPoint, and add the code in Figure 2.

The next object to create is a circle. The two critical definitional elements of a circle are its center and its radius. Of course, the center, itself, is a point. Create a Class module, name it GeoCircle, and add the code in Figure 3. While the area and the circumference of a circle are not needed for this example, they are very common properties, and are included in the code.

Figure 3
The only other property that needs to be added is setting the coordinates of the center given two points, P0 and P1. Figure 4 contains that code and it too goes into the GeoCircle class module. Don’t worry about the mathematics in it. The key element to note is that the function has two arguments, each of which is a GeoPoint. In addition, it uses the properties of the GeoPoint object to calculate midpoints, distances, and slopes of lines as needed. Finally, if there is an error it returns the error as a string message.
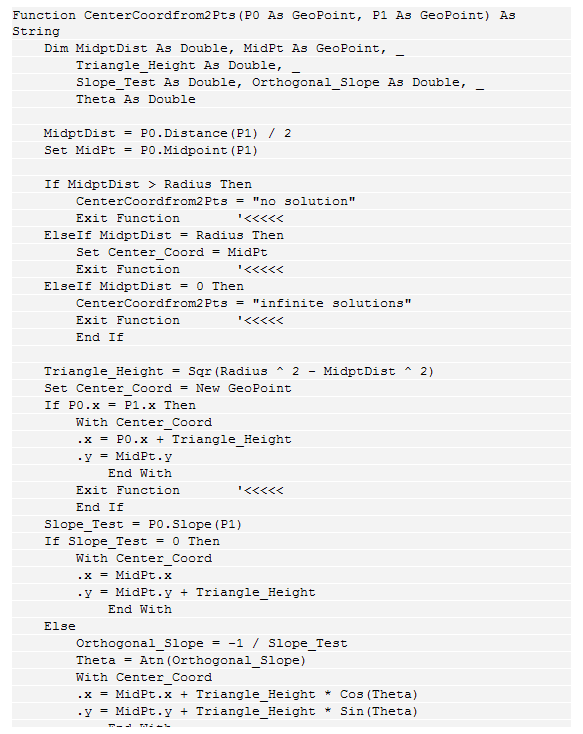
Figure 4
The above code yields some very easy to use capability that is available both from VBA and from Excel. In VBA, one can establish the center of a circle from its radius and two points with the code in Figure 5.
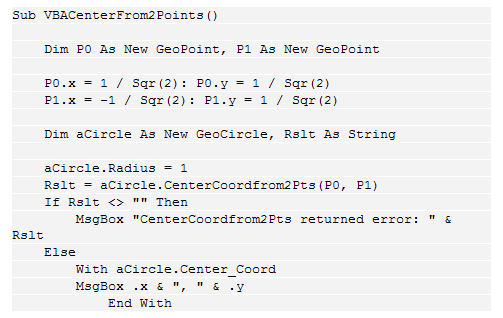
Figure 5
To use this new capability from an Excel worksheet, one needs a user-defined function. This will also serve as an interface between the Excel worksheet, which deals with cells laid out in a tabular fashion, and the custom classes used to solve the problem. In a standard module, enter the code in Figure 6.

Figure 6
This function, CenterFrom2Points is array-entered in two cells in a worksheet. These can be in the same row or in the same column as in Figure 7.
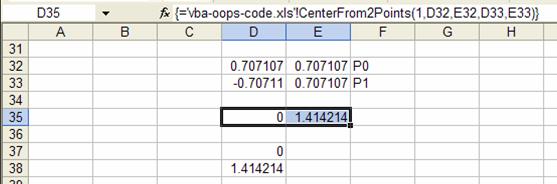
Figure 7