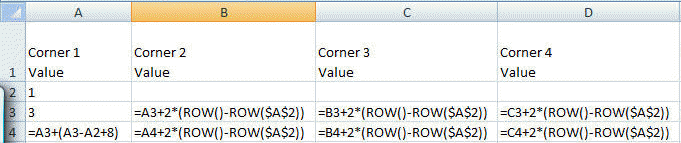
Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:
21 22 23 24
25
20 7
8 9
10
19 6 1
2 11
18 5
4 3
12
17 16 15 14
13
It can be verified that the sum of both diagonals is 101.
What is the sum of both diagonals in a 1001 by 1001 spiral formed in the same way?
The idea of simply filling out the 1001x1001 matrix was intimidating whether I did it by code or "by hand." A smarter approach seemed to be to figure out what the diagonal elements would be.
The numbers on the half-diagonal starting with 1 and moving towards the bottom right, are F0=1 F1=3 F2=13...Fi=Fi-1 + (Fi-1 + Fi-2 + 8) for i=2,3,...
The numbers on the half-diagonal starting with 1 and moving towards the bottom left are Gi=Fi+2*i.
Similarly, the numbers on the half-diagonal starting with 1 and moving towards the top left are Hi=Gi+2*i.
Finally, the numbers on the half-diagonal starting with 1 and moving towards the top right are Ji=Hi+2*i.
The last piece we need to recognize is that a 1001x1001 matrix will have 500 elements in each half-diagonal excluding the common center value of 1.
We can now set this up in Excel and solve the problem with no code support.
Start by entering the column headers and the values of F0 and F1. These are cells A2 and A3 respectively.
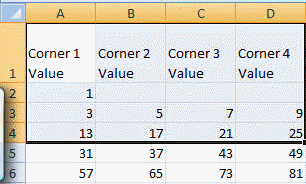
Calculate the values of G1, H1, and J1 (cells B3:D3 respectively) as well as the values in the next row (i.e., row 4) corresponding to i=2. Then, copy the contents of A4:D4 down to 5:205.
Finally, use the formula =SUM(A3:D502,A2) to get the desired result.