An irrational decimal fraction is created by concatenating the positive integers:
0.123456789101112131415161718192021...
It can be seen that the 12th digit of the fractional part is 1.
If dn represents the nth digit of the fractional part, find the value of the following expression.
d1 x d10 x d100 x d1000 x d10000 x d100000 x d1000000
The brute force VBA approach below took 200 seconds on my laptop. Of course, I could run it on the much faster desktop in under a minute but here's how to do it by hand:
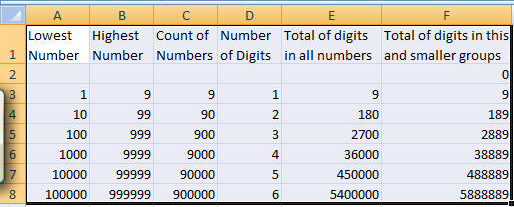
There are 9 numbers (1 through 9) with 1 digit each. In total they account for 9 digits.
There are 90 numbers (10 through 99) with 2 digits each. In total they account for 180 digits. Numbers with 1 or 2 digits account for 189 digits.
There are 900 numbers (100 through 999) with 3 digits each. In total they account for 2700 digits. Numbers with 1, 2, or 3 digits account for 2889 digits.
The table below lists the range of numbers required to get to 1,000,000 digits.
Now, in some other range, create the following:
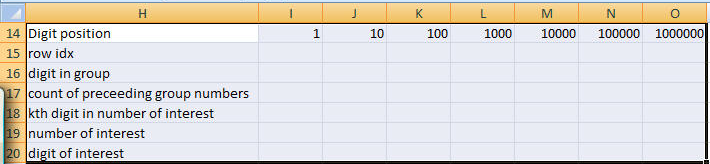
In I15:I20 enter the formulas

and copy them to J:O. The required result is the product of I20:O20.
Option Explicit
Option Base 0
Sub Euler040()
Dim IrrNbr As String, I As Long, ProcTime As Single
I = 1
ProcTime = Timer
Do While Len(IrrNbr) < 10 ^ 6
IrrNbr = IrrNbr & CStr(I): I = I + 1
Loop
Dim MultRslt As Integer
MultRslt = 1
For I = 0 To 6
MultRslt = MultRslt * CInt(Mid(IrrNbr, 10 ^ I, 1))
Next I
Debug.Print MultRslt, Timer - ProcTime
End Sub