Three distinct points are plotted at random on a Cartesian plane, for which -1000 ≤ x, y ≤ 1000, such that a triangle is formed.
Consider the following two triangles:
A(-340,495),
B(-153,-910), C(835,-947)
X(-175,41), Y(-421,-714), Z(574,-645)
It can be verified that triangle ABC contains the origin, whereas triangle XYZ does not.
Using triangles.txt (right click and 'Save Link/Target As...'), a 27K text file containing the co-ordinates of one thousand "random" triangles, find the number of triangles for which the interior contains the origin.
NOTE: The first two examples in the file represent the triangles in the example given above.
Researching the problem on the 'Net -- search Google for 'point in triangle' (w/o the quotes) -- shows that an easy approach is to ensure that three cross products have the same sign. Each cross-product is that of the vector representing one side of the triangle and the vector from the origin to the corresponding vertex. From http://mathforum.org/library/drmath/view/54505.html,
How can I know if D is inside the triangle or not?
A
/ \
/ \
/ D \
/_______\
C B
...
I will assume, for the moment, that the points A, B, and C are in
clockwise order around the triangle. If you look along AB from A
toward B, all points inside the triangle are on your right. Likewise
as you look along BC from B toward C, all interior points are on your
right; and the same for CA.
One way to calculate which side of the line a point is on is to take
the vector product or cross-product of two vectors. In particular,
construct the vectors B-A and D-A. I'll do this in three dimensions.
B-A = (x_b-x_a, y_b-y_a, 0)
D-A = (x_d-x_a, y_d-y_a, 0)
The cross-product of vectors (x_1, y_1, z_1) and (x_2, y_2, z_2) is
(y_1*z_2-z_1*y_2, z_1*x_2-x_1*z_2, x_1*y_2-y_1*x_2)
The cross product of two vectors is perpendicular to both vectors. Its
direction follows the right-hand rule: if the second vector is to the
left of the first (looking from above), then the cross product points
up.
Let's take the cross product (D-A)x(B-A). The x and y components are
zero; the vector points either up (z component is positive) or down
(z component is negative) depending on whether B-A is to the left or
right of D-A. Thus the sign of the z component of the cross product
tells us what we need:
z_ab = (x_d-x_a)*(y_b-y_a)-(y_d-y_a)*(x_b-x_a)
If z_ab > 0 then D is on the "inside" side of AB. If you do the same
replacing AB with CB and then CA, and each time z is negative, then D
is inside the triangle.
What if you don't know whether the vertices of the triangle are in
clockwise or counterclockwise order? Just change the condition: a
point D is inside the triangle if EITHER all of z_ab, z_bc, and z_ca
are positive, OR they are all negative. If the points are in clockwise
order, as I assumed above, then there is no (exterior) point such that
all the z's are negative, so we won't get spurious results due to the
broader condition.
Implementing the above requires minimal calculations and can be done in Excel without any code.
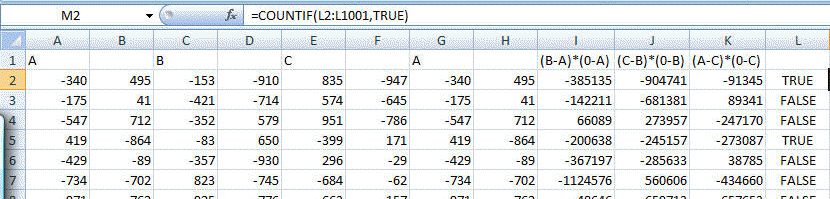
I downloaded and opened the triangles.txt file in Excel specifying that the comma was a field separator. The result was all the vertices showed up with one coordinate in one cell. To make life easy I added a header row. So, A:B represent the (x,y) coordinates of vertex A, Columns C:D represent the same coordinates of vertex B and columns E:F represent the coordinates for vertex C. Since our calculations will involve a symmetrical application of a vector-product formula, I duplicated the A vertex columns after the C vertex columns.
Then, to calculate the three cross-products, in J2 enter =(0-A2)*(D2-B2)-(0-B2)*(C2-A2). Copy J2 to L2 and N2 (skipping one column ensures that Excel adjusts the relative references in the copied formula by 2 columns). Then, delete the blank columns and in the now empty L2 enter the array formula =ABS(SUM(SIGN(I2:K2)))=3 -- to enter an array formula complete data entry with the CTRL+SHIFT+ENTER combination rather than just the ENTER or TAB key. If done correctly, Excel will show the formula enclosed in curly brackets { and }.
Copy I2:L2 down to 3:1001. In M2 enter the formula =COUNTIF(L2:L1001,TRUE) That's the required result.