A variable declared as type Variant can contain any type of data. This is unlike a variable that is declared as a specific type, say, String or Integer, which can only contain a text string or a specific range of integers, respectively. By contrast, a variant can contain any data – text, Boolean, an integer, or a real, i.e., a floating point, value. It can even behave like an array or an object, either a built-in Excel object or a user defined object. Essentially, there are almost no rules on what a developer can do with a variant. For example, with aVar declared as a variant each of the assignment statements is legitimate.
Dim aVar as Variant
aVar = "a"
aVar = 1
aVar = Array (1,22,333)
set aVar = ActiveSheet
aVar = 3.1415927
The common wisdom is that one should stay away from variants. By and large, that is true. If one knows the data type of a variable it is best to declare it correctly. There are many benefits to doing so, the most significant being that the VBA compiler can ensure data and program integrity[1]. With a variant one could accidentally assign a text string to what might be intended to be a number. Essentially, the developer gets the flexibility of a variable that can take any type of data together with the responsibility of ensuring proper data type use. That’s a steep burden and one best avoided whenever possible. Consequently, in those cases where the data type is pre-determined and will not change, it is indeed best to declare the variable of the particular type. [2]
However, there are many instances where a variant allows one to do things that otherwise would be impossible. The power of a variant comes from the fact that it is a simple data element and yet can contain any – and that means any – type of data. It can be a string or a Boolean or an integer or a real number. Hence, when the data type returned by a function can vary, one is obligated to use a variant for the returned value.
As we will see in a later section of this chapter, the ability to create an array in a variant makes it possible to create functions that would otherwise be impossible. For example, a function can return either an error condition or an array of values. It also allows a developer to write a User Defined Function (UDF) that returns multiple values in a single call to the function. A variant is also one way to pass an array as a ‘by value’ argument to a procedure. One Excel-specific reason to use a variant is that it provides a very efficient way to exchange information between Excel and VBA.
Finally, in the advanced section of the chapter, we will use the variant data type to create an array of arrays. This makes it possible to create, and work with, data structures that would otherwise be impossible. It also allows one to operate on an entire row of an array.
In the hands of a creative – and defensive – developer, the power of a variant can be nearly limitless.
Understanding a variant – a changing scalar
Understanding a variant – a scalar or an array
Comparing a dynamic array with a variant
Functions that return an array or a scalar
Returning an array as a function value and backward compatibility with Excel 97
Efficiently exchanging information with Excel
Passing an array as a ‘by value’ argument
Understanding a variant – implement an array of arrays
Half a matrix – track travel distances between cities
Preserve existing content while resizing any dimension of a matrix
Work with an entire row of an array
Martin S on Feb. 8, 2013:
I've stumblled upon this page and enjoyed reading your clear explanation, which proves that not only you KNOW what you're talking about, but also convey it just as well. GREAT job! Well Done!.
At the very basic level a variant is a type of variable that can contain any kind of data item. Effectively, the same variable can behave as a string or a number or a Boolean. This is very useful when working with a procedure that returns different types of values. One example of such a procedure is Excel’s InputBox method. If the user clicks the Cancel button, the function returns a False value. Otherwise, it returns whatever the user entered in the textbox as the datatype requested by the developer.
In Code Sample 1, one variable, Rslt, behaves as a String, a Double, a Boolean, or a Range object, depending on what the developer wanted and what the user does.
Option Explicit
Sub testInputBox()
Dim Rslt As Variant
Rslt = Application.InputBox("Please enter a number", Type:=1)
Debug.Print TypeName(Rslt)
Rslt = Application.InputBox("Please enter a string", Type:=2)
Debug.Print TypeName(Rslt)
Rslt = Application.InputBox("Please click the Cancel button", Type:=2)
Debug.Print TypeName(Rslt)
Set Rslt = Application.InputBox("Please select a range, then click OK", _
Type:=8)
Debug.Print TypeName(Rslt)
End Sub
The result of running the above code is shown below:
Double
String
Boolean
Range
This is the simplest way where a variant is not only useful but mandatory. No other datatype would suffice for the variable Rslt.
Please don’t misunderstand me. I am not advocating the willy-nilly reuse of the same variable in different roles. A variant is not meant to be a cheap trick to save a few bytes of memory. However, there are instances where it is necessary to use a variable that takes on different types depending on circumstance.
With an understanding of the simplest kind of variant under our belt, we move on to the use of variants as arrays.
In the previous section, we saw that a variant can contain different kinds of scalar variables. What might not have been evident is that the scalar does not have to be one of the “built-in” types. It can also refer to a custom object. The use of a variant in this instance is analogous to its use in the previous section. Given a class module named myClass with a property namedHeightInches, the following is valid.
Dim Rslt As Variant
Set Rslt = New MyClass
Debug.Print TypeName(Rslt)
Rslt.HeightInches = 65
Debug.Print Rslt.HeightInches
The result of running the above code would be:
MyClass
65
A big disadvantage of using a variant for an object is that one does not have access to the VBE’s Intellisense capability.
Next, we look at how a variant can also contain a complex data type such an array. This is an important stepping stone en route to unleashing the true power behind a variant data type.
Consider the code
Sub VariantAsArray()
Dim SomeVar As Variant
ReDim SomeVar(9)
SomeVar(9) = 81
MsgBox SomeVar(9)
End Sub
SomeVar is a variable of type Variant. Since a variant can behave like any data type, we can make it look like an array, which is exactly what the ReDim statement does. After it is executed, SomeVar becomes an array! Of course, we could create a 2 dimensional array with
ReDim SomeVar(9, 9)
One should also understand the conceptual difference between a variant that behaves like an array and an array that contains elements that are variants. Consider the following code:
Option Explicit
Sub VariantAndArrays()
Dim aVariantArray(2) As Variant
Dim aVar As Variant
ReDim aVar(2) As Long
Debug.Print TypeName(aVar), TypeName(aVar(2))
ReDim aVar(2) As String
Debug.Print TypeName(aVar), TypeName(aVar(2))
aVar = 10
Debug.Print TypeName(aVar)
End Sub
The results of the Debug.Print statements are shown below. Note that the variant aVar first contains an array of Long’s and then it morphs into an array of String’s. Yet, after the assignment of 10 to aVar, it now behaves like an Integer. Effectively, a variant can be not only a scalar but also an array.
Long() Long
String() String
Integer
By contrast, the variable aVariantArray is fixed as an array. Each element in it can be a different type, but the variable as a whole will always be an array. Effectively, we cannot add a line of code such as
aVariantArray = 10
As soon as we try to execute the code, VBA pops up with the error “Can’t assign to an array.” So, there is a difference between a variant that temporarily behaves like an array and a variable declared as an array. The latter cannot change its type.
Now that we have seen how a variant can behave like an array that we can resize as desired, one might compare it with a dynamic array. Is there a difference between a dynamic array and a variant that behaves like an array? Yes, there is. For the former, VB knows that it is an array and consequently expects the developer to treat it as such. By contrast, a variant is a variant that temporarily becomes an array. Consider the code below and the subsequent snapshots of the Locals window.
Sub DynamicArrAndVariant()
Dim anArr() As Variant, aVar As Variant
'anArr = 2
aVar = 2
ReDim anArr(2)
ReDim aVar(2)
End Sub
Just after the variables are allocated and before any assignment statements are executed, the Locals window shows:
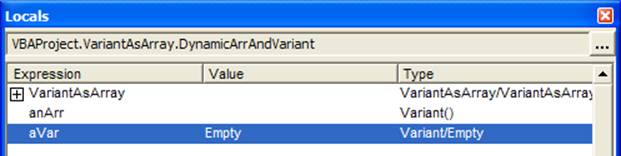
VBA knows that the anArr variable is an array and consequently shows the parenthesis in the Type column. Of course, since it doesn’t know the dimensions of the array, the parenthesis are empty. By contrast, VBA knows nothing about aVar other than it is a variant that is currently empty.
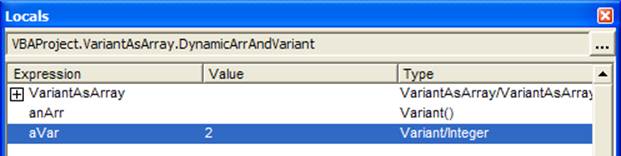
After the execution of the aVar=2 statement, VBA indicates that aVar is a variant that currently contains an integer (see below).
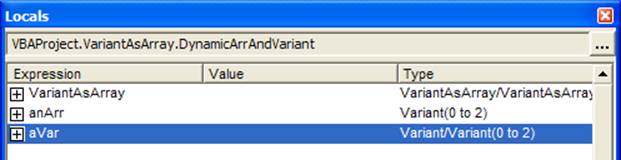
After both ReDims are executed, VBA knows that anArr is an array with 3 elements (indices 0, 1, and 2). It also knows that aVar is a variant that currently behaves like an array of 3 elements (again, indices 0, 1, and 2).
There are some Excel functions that return an array of values or a scalar such as a Boolean. And, of course, one can write a custom function that does the same. One built-in function that returns either an array or a scalar is the GetOpenFilename function. The only way to get the result of such a function is through a variant. Consider the code:
Sub demoGetFileOpenFilename()
Dim FileList As Variant
FileList = Application.GetOpenFilename(MultiSelect:=True)
End Sub
Step through the code twice. The first time select two filenames and check the Locals Window after the GetOpenFilename method is completed. FileList will appear as an array with each element containing a string value as shown in Figure 1
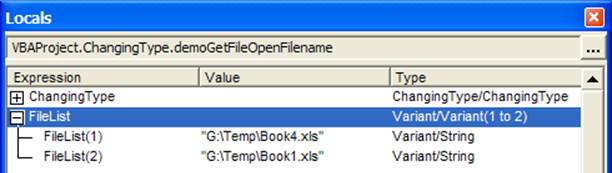
Figure 1
The second time around cancel the dialog box and once again check the Locals window after the method completes. This time FileList will appear to be a Boolean as shown in Figure 2.
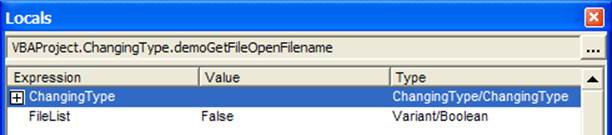
Figure 2
As we have already noted, there is nothing more useful for developing good software as using the correct data type. But, at times, a compromise is necessary to support some other capability. One such instance is returning an array result from a function while maintaining compatibility with Excel 97.
In VB6 (Excel 2000 and later), it is possible to declare the result of a function as an array type. For example, in the code below, the function SomeRandomNumbers returns an array of type single.
Function SomeRandomNumbers(HowMany As Long) As Single()
Dim I As Long, Rslt() As Single
ReDim Rslt(HowMany)
For I = LBound(Rslt) To UBound(Rslt)
Rslt(I) = Rnd()
Next I
SomeRandomNumbers = Rslt
End Function
However, VB5 (Excel 97) doesn’t support an array as a function return type. The above code would result in a syntax error. The work around would be to declare the return type as a variant and then create an array of type Single in that variant, as in the code below.
Function SomeRandomNumbersXL97(HowMany As Long) As Variant
Dim I As Long, Rslt() As Single
ReDim Rslt(HowMany)
For I = LBound(Rslt) To UBound(Rslt)
Rslt(I) = Rnd()
Next I
SomeRandomNumbersXL97 = Rslt
End Function
We have already seen how to create an array in a variant. Now, we explore the kind of data one can store in each element. Depending on the syntax of the ReDim statement, it can, obviously, be a variant. That leads us to a very powerful capability: the concept of “an array of arrays.” Consider, for example,
Dim SomeVar As Variant
ReDim SomeVar(9)
Since each element is a variant, the same rules that apply to the variable itself now apply to each individual element. Hence, we should be able to assign an array to each element itself. Unfortunately, we need to do this indirectly since we cannot use the ReDim statement directly. Using ReDim with element 9 of SomeVar to create an array as below generates a syntax error.
redim somevar(9)(9)
The VBA compiler doesn’t understand that the first set of parenthesis – SomeVar (9) – simply identifies one element of SomeVar and the 2nd set of brackets specifies the dimension of the array we want to create in this variant. So, we use a slight detour that illustrates, as we will explore in more detail later, another powerful capability of variants.
Sub addAnArrayToAnArray()
Dim SomeVar As Variant, Temp As Variant
ReDim SomeVar(9)
ReDim Temp(8)
SomeVar(9) = Temp
SomeVar(9)(8) = 72
MsgBox SomeVar(9)(8)
End Sub
In Code Sample 2 the first 3 lines of the subroutine simply change each of the variants SomeVar and Temp to an array. The next statement will be new to some readers. It assigns the entire array Temp to just one variable, i.e., SomeVar (9). If we look at the local variables just after this line of code is executed (use View | Local Windows) we would see
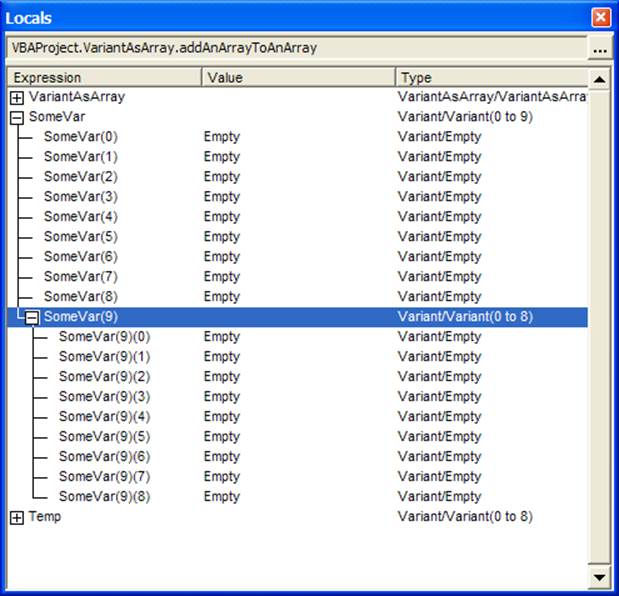
Figure 3
There are several important things to note in Figure 3.
First, SomeVar looks like a regular array and each element can be accessed with SomeVar (<index>) such as SomeVar (9).
Second, since each element is a variant in itself, they don’t have to look or behave identically to each other. For example, in Figure 3 all the elements are empty except the last element. That single element contains an entire array in it!
Third, note how VBA identifies each element of the array embedded inside of SomeVar (9). It is important to understand this. SomeVar(9) identifies one element of the array in SomeVar. This element is itself of a Variant type. Then we inserted a complete array into this single element. So, SomeVar(9) identifies the element of SomeVar and SomeVar(9)(8) identifies the element of the array inserted into this element. This is very different from a 2-dimensional array where one would use Array2D (9,8) to identify a particular element. What we have here is not a 2D array but an array of arrays! Figure 4 illustrates the concept of an array of arrays.
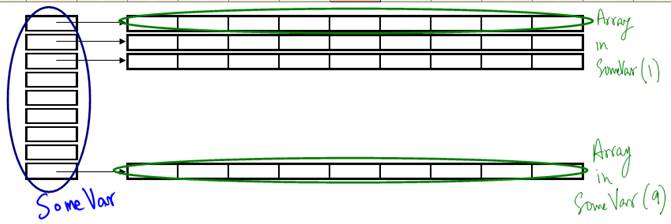
Figure 4
The astute reader may have already picked up on an important capability. It is eminently possible for each element of SomeVar to contain an array of a different size! We will see a practical application of this capability in the next section.
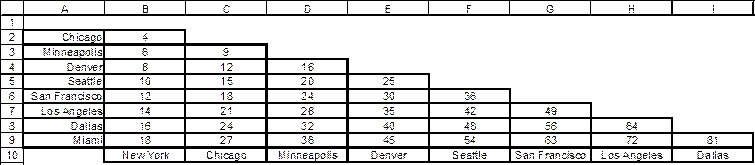
Figure 5
Figure 5 shows a very common way of showing distances between various cities. While the overall figure may appear to be a two dimensional matrix, it is only the bottom half that is really used. If one wanted to use a 2D array it would be declared as
Dim CityDistances(1 To 8, 1 To 8) As Long.
However, that is not an ideal data structure because it doesn’t reflect the true intent of the application, which requires a triangular matrix, which as the correct data structure for this application makes the code that much more self-documented and easily understood. We can create this data structure, where the number of elements in the 2nd dimension of the matrix equals the index of the first dimension with the code in Code Sample 3. A secondary benefit is the associated performance savings. The triangular matrix has only ˝ the number of elements of the more traditional matrix and consequently uses about ˝ the memory.
In the following code sample, the function TriangularMatrix creates a variant array called FirstDimension that is the size requested by the calling procedure. It then proceeds to embed an array in each of those elements. Each of these embedded arrays has a size equal to the index of the first dimension.
Option Explicit
Function TriangularMatrix(ByVal nbrRows As Long)
Dim FirstDimension() As Variant, i As Long, TempArr() As Variant
ReDim FirstDimension(1 To nbrRows)
For i = LBound(FirstDimension) To UBound(FirstDimension)
ReDim TempArr(1 To i)
FirstDimension(i) = TempArr
Next i
TriangularMatrix = FirstDimension
End Function
Sub CityDistancesInfo()
Dim CityDistances As Variant
CityDistances = TriangularMatrix(8)
CityDistances(3)(1) = 8
MsgBox CityDistances(3)(1)
End Sub
Figure 6 shows the data structure created by the TriangularMatrix function. The first element of CityDistances contains an embedded array of size 1. The 2nd element contains an embedded array of size 2 all the way to the eighth element, which contains an array of size 8. We should re-emphasize the difference between how one addresses the elements of this triangular matrix and a traditional 2D matrix. In the case of a regular matrix, one would use CityDistances (3,1) for the 1st element of the 3rd row. However, in the case of the triangular matrix, each dimension is created independently. Consequently, the VBA compiler only knows that we created a one dimensional array of type variant and then embedded an array in each element. The addressing of the matrix has to reflect the nature of how it was created. One would use CityDistances(3)(1) – just as shown in the Locals dialog box in Figure 6 – to get at the same element as the traditional CityDistances (3,1). The first number, (3), indexes the 3rd element of the variant array. The next (1) indexes the array embedded in that element.
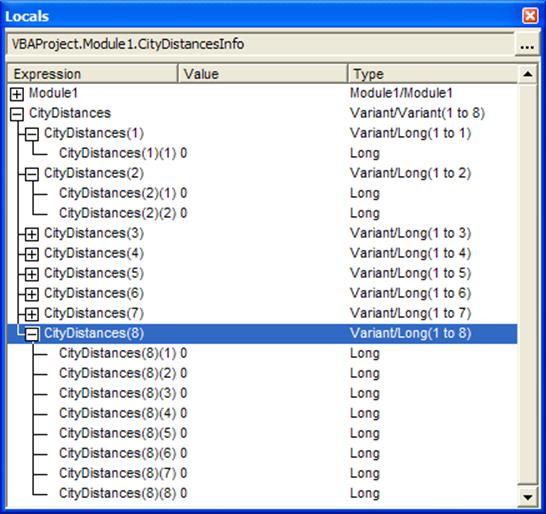
Figure 6
With a traditional multi-dimensional matrix it is not possible to preserve the existing data and change the size of any dimension but the last. For example, in Code Sample 4, the Redim Preserve line generates a ‘Subscript Out of Range’ error.
Sub failRedimPreserve()
Dim SomeArr()
ReDim SomeArr(1 To 10, 1 To 10)
ReDim Preserve SomeArr(1 To 11, 1 To 10)
End Sub
By contrast, if one implements the 2D array as an array of arrays, it is eminently possible to change the “first” dimension while preserving the existing data. In the code below, the function create2DMatrix creates an array of 10 elements in the variable SomeArr. Then, it inserts an array of size 9 in each of those (variant) elements. The addTestData subroutine initializes the “array of arrays” with some data. The next statement changes the dimension of the SomeArr array to 11 and the next statement copies the content of SomeArr(10) into the new element SomeArr(11). Of course, since SomeArr(10) contains an array, we have effectively inserted an array into SomeArr(11) as shown in Figure 7.
Sub VariantRedimPreserve()
Dim SomeArr()
SomeArr = create2DMatrix(10, 9)
addTestData SomeArr
ReDim Preserve SomeArr(1 To 11)
SomeArr(11) = SomeArr(10)
End Sub
Code Sample 5
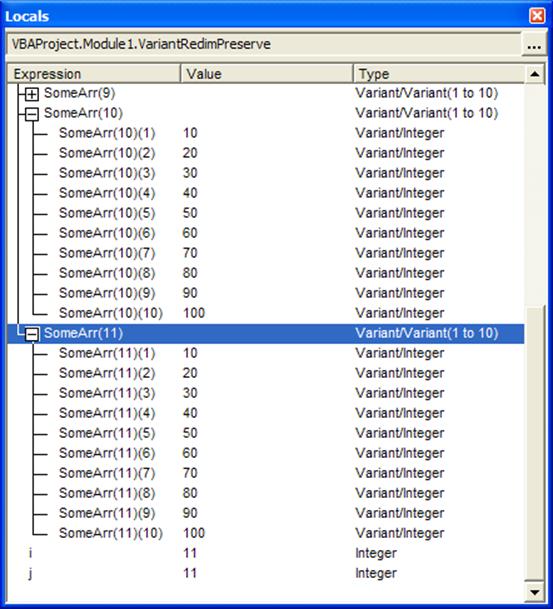
Figure 7
The previous example also demonstrated another powerful capability of the array of arrays concept. Since each dimension in an array of arrays is independent of the others, it is possible to treat an entire row as a single element for certain types of operations. This allows us to apply a function to an entire row. Or, even swap to rows with simple assignment statements. In the previous section, we used the assignment statement SomeArr(11) = SomeArr(10). By simple extension, one can use a temporary variant and implement a swap that looks very much like that for two scalar variables. What would a scalar swap look like?
Of course, assignment statements are only one possibility. To sum each row of a 2D matrix implemented as an array of arrays, one would use the subroutine below. In contrast to the traditional 2D matrix that would need two loops one embedded in the other, the code below uses a single loop and the Excel SUM function.
Option Explicit
Sub SumARow()
Dim a2DArr, I As Integer
a2DArr = create2DMatrix(8, 9)
addTestData a2DArr
For I = LBound(a2DArr) To UBound(a2DArr)
Debug.Print Application.WorksheetFunction.Sum(a2DArr(I))
Next I
End Sub
[1] A secondary benefit is that the compiler and the hardware may be able to improve code execution.
[2] The issue of data type is a bit more complex than we need to delve into in this chapter. Suffice it to say that if your program performance depends on whether your data items are byte-aligned or word-aligned at the hardware level, you have more fundamental issues to address. There are those who will tell you to always use the most hardware “efficient” data type but that is fool’s gold. If you have a variable that should take values between 0 and 255 you should use a Byte data type. The fact that the compiler (and the OS) will use the same amount of hardware space as for a Long data type is completely irrelevant. Far more important is the system’s assurance that your variable will never take a negative value or a value greater than 255!
In fact, the very concept of numeric data types being limited to Byte, Integer, Long, Single, or Double is more of a archaic leftover from the early days of computing than anything else. It is unfortunate that no widely used programming language implements a true specification for numeric data. If a programmer wants an index for the months of the year, the ideal specification would be
MonthIdx Integer 1..12
Similarly, if one were generating random numbers between -100 and +100, the ideal variable would be
RandomValue Real -100..100
An alternative specification that would take into account that the random numbers would be greater than or equal to -100 and strictly less than 100 would be:
RandomValue Real [-100..100)
Of course, since neither VB nor VB.Net support such a declaration, there is not much one can do except choose the most restrictive data type from a woefully limited menu of Byte, Integer, Long, Single, and Double.