You are on the Home/Other Tutorials/Project Euler/Problem 58 page

Project Euler - Problem 58

Problem description

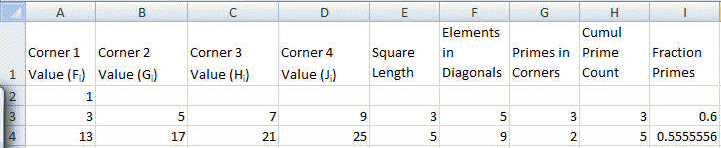
Starting with 1 and spiralling anticlockwise in the following way, a square spiral with side length 7 is formed.

37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49

It is interesting to note that the odd squares lie along the bottom right diagonal, but what is more interesting is that 8 out of the 13 numbers lying along both diagonals are prime; that is, a ratio of 8/13 62%.

If one complete new layer is wrapped around the spiral above, a square spiral with side length 9 will be formed. If this process is continued, what is the side length of the square spiral for which the ratio of primes along both diagonals first falls below 10%?

Solution

While the spiral in this case is anti-clockwise, the calculation of the elements on the diagonals is identical to that for Euler 28. This can be done in Excel with the help of the IsPrime user defined function as long as the numbers in question are not longer than 15 digits in length. Alternatively, one can use VBA and the decimal data type that supports 29 significant digits.

Function IsPrime(aNbr As Variant) As Boolean
    Dim K As Long
    K = 1
    If aNbr = 2 Or aNbr = 3 Then IsPrime = True: Exit Function
    If aNbr Mod 2 = 0 Or aNbr Mod 3 = 0 Then IsPrime = False: Exit Function
    Do While 6 * K - 1 <= Sqr(aNbr)
        If aNbr Mod (6 * K - 1) = 0 Or aNbr Mod (6 * K + 1) = 0 Then _
            IsPrime = False: Exit Function
        K = K + 1
        Loop
    IsPrime = True
    End Function
Sub Euler058()
    Dim SqrLen As Long, CellVal As Variant, PrevCellVal As Variant, _
        NbrPrimes As Long, NbrDiagCells As Long, _
        ProcTime As Single
    ProcTime = Timer
    CellVal = CDec(3): PrevCellVal = CDec(1)
    NbrPrimes = 3: NbrDiagCells = 5
    SqrLen = 3
    Do While NbrPrimes / NbrDiagCells >= 0.1
        SqrLen = SqrLen + 2
        NbrDiagCells = 2 * SqrLen - 1
        Dim Temp As Variant
        Temp = CellVal + (CellVal - PrevCellVal + 8)
        If IsPrime(Temp) Then NbrPrimes = NbrPrimes + 1
        If IsPrime(Temp + ((SqrLen - 3) / 2 + 1) * 2) Then NbrPrimes = NbrPrimes + 1
        If IsPrime(Temp + ((SqrLen - 3) / 2 + 1) * 4) Then NbrPrimes = NbrPrimes + 1
        If IsPrime(Temp + ((SqrLen - 3) / 2 + 1) * 6) Then NbrPrimes = NbrPrimes + 1
        PrevCellVal = CellVal: CellVal = Temp
        Loop
    Debug.Print SqrLen, Timer - ProcTime
    End Sub

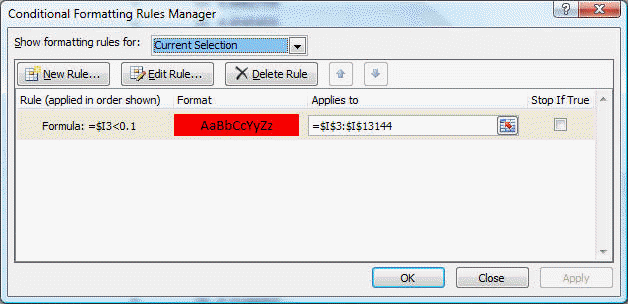
In Excel, start with the layout for Euler 28 and add the extra columns shown below. Copy the contents of row 4 as far down as necessary to get a value < 10% in column I. Use conditional formatting for column I to spot the instances with under 10% of primes.